Potential-based Reward Shaping for Larger State Spaces

One of the best things about taking Georgia Tech CS Masters is that, there's always something new to you that you can explore and try in your project assignments. And this is one of those things that was new to me: using Potential-based Rewards Shaping to improve the performance of our beloved Q-Learning algorithm. In this project, I will be using Q-Learning to solve the Frozen Lake environment.

1. About the Environment

In the frozen lake problem, the agent must navigate across a frozen lake represented by a grid, from a starting point to a goal location, while avoiding holes in the ice. The state space consists of a grid of size NxN, where each cell can either be a frozen surface, a hole, or the goal. The agent can move up, down, left, and right. As the surface is slippery, the agent will move in the intended direction with probability $\frac{1}{3}$, or else it will slip and move in either perpendicular direction with equal probability $\frac{1}{3}$. Agent receives 0 reward points for landing on a frozen surface or hole, and gains +1 reward point for reaching the goal. Each episode, the agent starts from [0, 0]. When on a frozen surface, the agent can take action to move toward the goal. The game ends if the agent reaches the goal or drops into the hole (oh no! man overboard!).

This problem is interesting as it is a simple and well-understood example that can be easily visualized to facilitate algorithm analysis. In addition, the problem size is adjustable to facilitate analysis concerning problem size.

The FrozenLake-v1 environment is loaded from gymnasium library. Map sizes 4x4 and 10x10 will be used int this study to analyze what performance gains does potential-based reward shaping provides.

2. Algorithm

An implementation of the Q-Learning algorithm is adapted from the bettermdptools Python library. I will be modifying the algorithm to include reward shaping, and then compare the original and modified versions for our analysis.

Q-Learning. Q-Learning is a popular model-free reinforcement learning algorithm used to find the optimal action-selection policy for a given environment. It works by estimating the Q-value (action-value), which represents the expected cumulative reward of taking an action 𝑎 a in a state 𝑠 s and following the optimal policy thereafter. The Q-value is updated iteratively using the Bellman equation: $Q(s, a) \leftarrow Q(s, a) + \alpha \left[ r + \gamma \max_{a'} Q(s', a') - Q(s, a) \right]$. Personally, I find David Silver's Lectures to explain the entire RL basics really, really well along with illustrations.

Potential-based Reward Shaping. From Ng et al. (1999), Potential-based reward shaping is a technique in reinforcement learning used to guide an agent's learning process by modifying the reward function without altering the optimal policy of the environment.

In this experiment, I calculate the state potential for a given state as the Manhattan distance between the goal and the state. The closer the state is to the goal, the higher the state potential will be. Given TD-update portion of the original Bellman equation, we can simply modify this to include the potential value, thus our new TD-update portion becomes: $r + F(s, s') + \gamma \max_{a'} Q(s', a') - Q(s, a)$. The potential function $F(s, s')$ can be calculated as the difference between the potential value at s and s' (discounted): $F(s, s') = \gamma \Phi(s') - \Phi(s)$, where $\Phi(s)$ would be a reward score given the distance between the goal and the state:

def potential_func(s: np.array, goal: np.array, map_width: int, map_height: int) -> float:
    dist_from_goal = np.sum(np.abs(goal - s))  # Distance from goal
    max_dist = (map_width + map_height - 2)  # Maximum distance possible
    return 1.0 - (dist_from_goal / max_dist)

As we have noticed, a discounting factor $\gamma$ is also applied on the potential value of the next state: $\gamma \Phi(s')$. This means we are also balancing the tradeoffs between immediate and future potentials, just as we do for immediate and future rewards in the original Bellman equation.

3. Results and Analysis

With all that implemented, I tested out both original and modified versions of the Q-Learning algorithms on two environments, one with 4x4 size and another with 10x10 size. And finally here are the results:

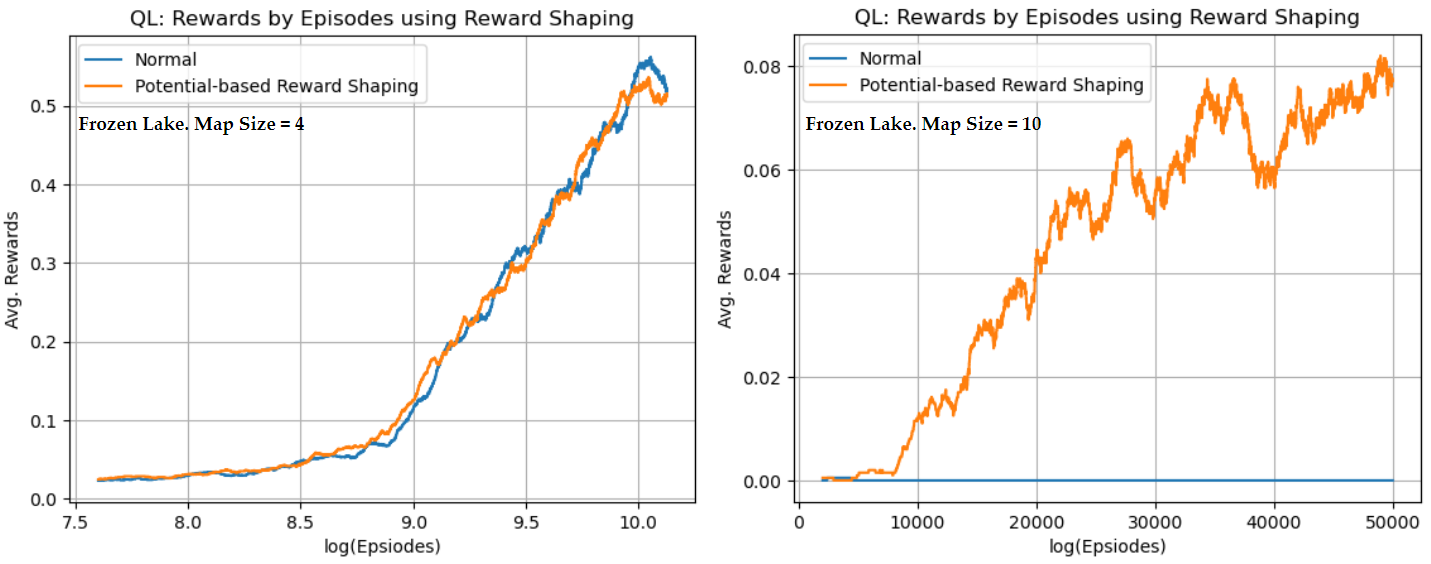
Fig 1a. FrozenLake 4x4 Comparison Results

The two charts above compares the normal Q-learning algorithm with modified version of Q-learning with Potential-based Reward Shaping.

Map size 4x4 (left chart) Both algorithms appear to be performing similarly. Although, reward shaping seems to provide tiny slight improvement in earlier episodes, but it is not very much different. Thus here, it's not much of any improvement.

Map size 10x10 (right chart) Reward shaping significantly improves the convergence rate compared to normal Q-learning. We can see that Normal Q-learning struggles to improve its average reward, remaining almost flat throughout the training process. In contrast, reward shaping has enabled the agent to achieve higher rewards faster and consistently increases the performance over episodes.

4. Summary

Potential-based Reward Shaping is highly beneficial in environments with larger state spaces or higher complexity. From this experiment, it has significantly improved the convergence rate. By providing some sort of guidance towards the goal, reward shaping can help agents learn better and converge faster. Whereas in simpler, less complex environments, it's usefulness and effectiveness could be pretty much minimal.

References: