- Published on
Measuring Cannibalization and Optimizing for Product Portfolio
- Authors

- Name
- Kenneth Lim
Price optimization is the process of determining the ideal price point for a product or service to maximize business objectives such as revenue, profit, or market share. It involves analyzing various factors, including market demand, customer behavior, competitor pricing, and cost structures, to identify pricing strategies that deliver optimal results.
One critical consideration in price optimization is cannibalization. Cannibalization refers to the phenomenon where the sales or profits of one product decrease due to the introduction, pricing changes, or promotion of another product in the same portfolio. While businesses often aim to maximize revenue across their product lines, failure to account for cannibalization can possibly erode overall profitability.
In this post, I will demonstrate profit optimization at the individual product level and highlight how optimizing prices for individual products might inadvertently reduce overall profitability. I will then shift the focus to portfolio-level optimization to explore how a holistic approach can drive a significant uplift in overall profits.
1. Data Generation
To start off, we can generate a synthetic dataset using the data generation function from the previous post. For simplicity, a dataset without trend, seasonality and holiday components can be generated for three related substitute products.
2. Model Fitting
Next, we can use a straightforward Bayesian regression model to capture each product’s baseline demand, price elasticity, and cross elasticities. By leveraging on Bayesian models, it allows us to quantify uncertainty around demand, price, and cross elasticity parameters, enabling a more robust understanding of how pricing decisions for any one product can influence overall sales across the three related products.
To make use of our model for inference, we can also define a function that performs counterfactual predictions for demand given a set of prices and costs:
Although the model generates predictions for every time period, our example and the data generated assumes constant elasticity. Thus we can simply focus our analysis on just any one day. Here, I’ll simply use the results from the first day for comparison.
With that all set up, we can now start our analysis on optimizing prices. Let's go :)
3. Context Setting
In this exercise of profit optimization, say a company is has three similar products with the following current prices and costs:
- Product 1 — Price: $125, Cost: $110
- Product 2 — Price: $275, Cost: $120
- Product 3 — Price: $325, Cost: $130
4. Optimizing at Product-Level Profit
By performing a quick grid search for each product at different price points, we can easily find the product-level optimal price that maximizes profit for that product, and use the optimal prices that we've found to calculate the new overall profit. Results can be seen below:
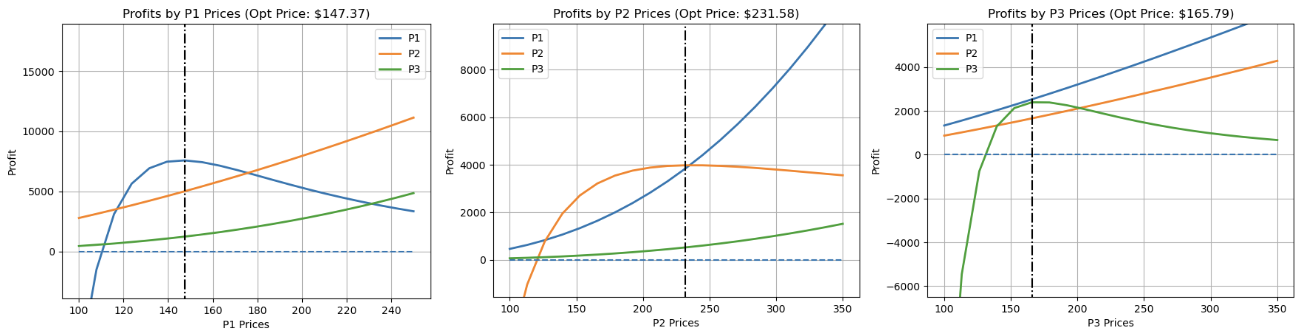
Figure 1. Product-Level Optimal Prices
| Qty | Revenue | Profit | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Orig. Prices | Opt. Prices | Δ% | Orig. Prices | Opt. Prices | Δ% | Orig. Prices | Opt. Prices | Δ% | |
| P1 | 395 | 56 | -86% | $49,341.62 | $8,233.22 | -83% | $5,920.99 | $2,087.71 | -65% |
| P2 | 25 | 19 | -24% | $6,919.77 | $4,490.65 | -35% | $3,900.24 | $2,163.68 | -45% |
| P3 | 4 | 65 | 1525% | $1,340.52 | $10,832.81 | 708% | $804.31 | $2,338.51 | 191% |
| Overall | 424 | 141 | -67% | $57,601.91 | $23,556.68 | -59% | $10,625.54 | $6,589.90 | -38% |
Table 1. Results based on applying all Product-Level Optimal Prices for P1, P2, and P3
Product 1. Based on the product-level optimal price, the price of Product 1 would need to be increased from $125.00 to $147.37. This price increase may prompt some customers to switch to Product 2 or Product 3, thereby increasing the quantity sold and profits for those two products. Overall, raising the price of Product 1 seems to have a net positive impact on overall profitability.
Product 2 and 3. Conversely, the product-level optimal prices for Products 2 and 3 suggest a price reduction. Specifically, the price of Product 2 would drop from $275.00 to $231.58, and the price of Product 3 would decrease from $325.00 to $165.79. These price reductions could potentially cannibalize sales of Product 1 and also affect the sales of Products 2 and 3 themselves. The key question for profit maximization is whether the increase in profits for Products 2 and 3 outweighs the negative impact of cannibalization on all three products.
Measuring Cannibalization Effects. To measure the cannibalization effects among Products 1, 2, and 3, we can compare the predicted overall profits generated by the original prices with those achieved using the new optimal prices. The difference in overall profits represents the cannibalization effect. According to the results in Table 1, the cannibalization effect amounts to $4,035.64 (calculated as $10,625.54 - $6,589.90).
The analysis demonstrates that while optimizing prices at the individual product level can yield increased profitability for certain products, it also introduces the risk of significant cannibalization effects across the product portfolio. For Product 1, the price increase appears to have a net positive impact on overall profitability, primarily due to increased sales and profits for Products 2 and 3. However, the price reductions for Products 2 and 3 lead to a notable cannibalization effect, resulting in an overall profit decrease of $4,035.64.
This highlights the importance of adopting a portfolio-level pricing strategy that considers interdependencies between products, ensuring that the combined profitability across all products is maximized rather than focusing solely on individual product gains.
5. Optimizing at Portfolio-Level Profit
We now consider the overall profit across all three products to identify the optimal prices for P1, P2, and P3. This involves performing a grid search over all possible price combinations and calculating the total profit for each scenario.
After completing the grid search, the portfolio-level optimal prices identified are:
- Product 1 — Price: $250.00
- Product 2 — Price: $350.00
- Product 3 — Price: $175.76
| Qty | Revenue | Profit | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Orig. Prices | Opt. Prices | Δ% | Orig. Prices | Opt. Prices | Δ% | Orig. Prices | Opt. Prices | Δ% | |
| P1 | 395 | 20 | -95% | $49,341.62 | $5,053.93 | -90% | $5,920.99 | $2,830.20 | -52% |
| P2 | 25 | 20 | -20% | $6,919.77 | $7,047.50 | 2% | $3,900.24 | $4,631.21 | 19% |
| P3 | 4 | 594 | 14750% | $1,340.52 | $104,393.84 | 7688% | $804.31 | $27,178.40 | 3279% |
| Overall | 424 | 634 | 50% | $57,601.91 | $116,495.27 | 102% | $10,625.54 | $34,639.81 | 226% |
Table 2. Result based on applying Profits using Portfolio-Level Optimal Prices
Product 1. Under the portfolio-level optimization, the price increase for Product 1 results in a significant reduction in quantity sold, dropping from 395 units to just 20 units (-95%). This leads to an overall decline in revenue (-90%) and profit (-52%) for P1. However, the reduced availability of P1 creates an opportunity for customers to shift toward Products 2 and 3, which offsets some of the losses.
Product 2. For Product 2, the optimal price adjustment involves a slight decrease, resulting in a 20% reduction in quantity sold. Despite this, revenue for P2 increases marginally by 2%, and profit improves significantly by 19%, demonstrating that the lower price makes the product more attractive to customers while maintaining strong profitability.
Product 3. Product 3 shows a dramatic increase in quantity sold, skyrocketing by 14,750%, as its price is significantly reduced. This leads to a massive 7,688% increase in revenue and a 3,279% boost in profit. P3 becomes a key driver of portfolio-level profit growth under the optimized pricing strategy, as its lower price captures more demand and generates exceptional returns.
Overal Impact. At the portfolio level, the optimization strategy increases total quantity sold by 50%, from 424 units to 634 units. Revenue doubles, growing by 102%, and overall profit experiences a substantial uplift of 226%, rising from 34,639.81. These results highlight the effectiveness of a holistic, portfolio-level pricing strategy in maximizing overall profitability, even when individual products may experience declines.
Overall, the price increase for P1 shifts demand to P2 and P3, demonstrating the importance of managing product interdependencies in pricing decisions. While P1 experiences declines in quantity, revenue, and profit, the gains from P2 and especially P3 more than compensate for these losses. Optimizing prices across the portfolio enables significant profit growth (+226%) compared to individual product-level optimization.
Summary
Here I have explored the impact of price optimization at both individual product and portfolio levels:
- Initially, product-level optimization was performed, revealing that focusing solely on individual products can lead to cannibalization and an overall reduction in profits
- To address this, portfolio-level optimization was applied by conducting a grid search to find optimal prices across all products, resulting in significant increases in overall quantity sold, revenue, and profit.
Thanks for reading this far if you've made it here, I hope this has been useful and have a great day!