Refuting Causal Effect Estimates

I've written quite a few posts on estimating causal effects previously. In this post, I'm going to write about how we can go about testing our causal effect estimates.

In the real world, we can never be sure if our model free from issues such as omitted variable bias from unobserved confounders, incorrect model specification, endogeneity, collider or mediator biases, spurious correlations, regularization biases, etc... Thus, testing and refuting causal estimates in causal inference is a crucial step because it helps to ensure the reliability, validity, and robustness of the conclusions drawn.

The methods below are referenced from DoWhy documentation.

Refutation Tests

Using synthetic data, I will be demonstrating a few refutation tests on our previous estimates obtained through OLS and ML methods.

Based on Negative controlled

A refutation test based on negative controls evaluates the robustness of causal estimates by introducing variables or scenarios that are known to have no causal relationship with the outcome, thus the name "negative controls".

Let's define a simulation function that generates multiple estimates using the test function and perform a one-sample t-test. If the p-value is < 0.05, then the model fails the refutation test, indicating there is an issue with the model.

def run_ols(dataset):
    target = "ln_demand"
    predictors = " + ".join([c for c in dataset.columns if c != target])
    model = smf.ols(f'{target} ~ {predictors}', data=dataset).fit()
    pe_coef = model.params['ln_price']
    return pe_coef


def run_refutation_test(dataset, test_fn, expected_value=0, n_runs=50):
    estimates = np.array([test_fn(dataset, seed=seed) for seed in np.arange(n_runs)])
    _, p_val = ttest_1samp(estimates, expected_value)
    if p_val < 0.05:
        print(f"Failed: {test_fn.__name__}. (p-value: {np.round(p_val, 5)})")
    else:
        print(f"Passed: {test_fn.__name__}. (p-value: {np.round(p_val, 5)})")

Let's get our casual estimate using OLS and take note:

expected_pe_coef = run_ols(dataset)
expected_pe_coef

> -0.06001771813331931

Placebo Treatment. What happens to the estimated causal effect when we replace the true treatment variable with an independent random variable? We should expect that the effect should go to zero, since a random treatment should result in zero effect on the outcome. This serves as a test to determine if the causal estimation method is robust and appropriately detects genuine causal relationships.

def placebo_test(dataset, seed=0):
    np.random.seed(seed)
    df = dataset.copy()
    df['ln_price'] = np.random.permutation(df['ln_price'].values)
    return run_ols(df)

run_refutation_test(dataset, placebo_test, expected_value=0)

> Passed: placebo_test. (p-value: 0.62363)

Dummy Outcome. What happens to the estimated causal effect when we replace the true outcome variable with an independent random variable? We should expect that the effect should go to zero, since a random outcome should have zero relation to the treatment. This test ensures the causal inference method is able to distinguish true causal effects from random noise, and not detecting false relationships.

def dummy_outcome_test(dataset, seed=0):
    np.random.seed(seed)
    df = dataset.copy()
    df['ln_demand'] = np.random.permutation(df['ln_demand'].values)
    return run_ols(df)

run_refutation_test(dataset, dummy_outcome_test, expected_value=0)

> Passed: dummy_outcome_test. (p-value: 0.40133)

Random Common Cause. Does the estimation method change its estimate after we add an independent random variable as a common cause to the dataset? We should not expect the causal estimate to change, since an addition of random variable to the model should have no impact/influence on the causal estimate. This test ensures the causal estimate from the model is unaffected by spurious variables.

def random_common_cause_test(dataset, seed=0):
    np.random.seed(seed)
    df = dataset.copy()
    df['X'] = np.random.normal(0, 1, size=df.shape[0])
    return run_ols(df)

run_refutation_test(dataset, random_common_cause_test, expected_value=expected_pe_coef)

> Passed: random_common_cause_test. (p-value: 0.28463)

Data Subsample. Does the estimated effect change significantly when we replace the given dataset with a randomly selected subset? We expect the estimate not change significantly. This test can be used to address selection bias or unbalanced covariates where the treatment and control groups differ significantly. Small datasets or datasets with high dimensionality may lead to higher variability in estimates when subsampling.

def data_subsample_test(dataset, seed=0):
  df = dataset.sample(frac=1.0, replace=True, random_state=seed)
  return run_ols(df)

run_refutation_test(dataset, data_subsample_test, expected_value=expected_pe_coef)

> Passed: data_subsample_test. (p-value: 0.11496)

Based on Sensitivity Analysis

Simulation-based sensitivity analysis evaluates the robustness of causal estimates by simulating hypothetical scenarios where unobserved confounders might exist. This involves generating synthetic data that includes the effects of potential confounders on both the treatment and the outcome. We can vary the simulated confounder effects to observe how the causal estimate changes. This method can provide more flexibility in testing a range of confounders, offering a better understanding of how confounding impacts causal estimates.

In this section, I will be using DoWhy a well-established causal inference library to perform sensitivity analysis. For effect strength of treatment, I will be simulating at strong effect up to $\pm 0.6$. For effect strength of outcome, referencing to our causal estimate of $0.6$, I will simulate at relatively strong levels as well at $\pm 0.08$.

import networkx as nx
from dowhy import CausalModel

causal_graph = nx.DiGraph([(c, "ln_demand") for c in dataset.columns if c != "ln_demand"])
model = CausalModel(
   data=dataset,
   treatment="ln_price",
   outcome="ln_demand",
   graph=causal_graph,
)

identified_estimand = model.identify_effect()

estimate = model.estimate_effect(identified_estimand,
    method_name="backdoor.linear_regression",
    test_significance=True
)

res_unobserved_range=model.refute_estimate(
    identified_estimand,
    estimate,
    method_name="add_unobserved_common_cause",
    confounders_effect_on_treatment="linear",
    confounders_effect_on_outcome="linear",
    effect_strength_on_treatment=np.linspace(-0.6, 0.6, 11),
    effect_strength_on_outcome=np.linspace(-0.08, 0.08, 11),
    plot_estimate=False,
)

print(res_unobserved_range)

> Refute: Add an Unobserved Common Cause
> Estimated effect:-0.06002434202555751
> New effect:(-0.10092959905198384, 0.017440513524050516)

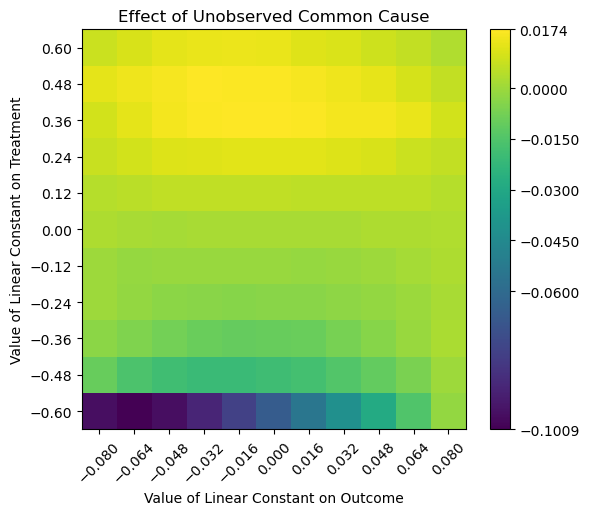
Figure 1. New Effect Estimates under Unobserved Common Cause

From the above, we can see that the new range of the estimated effect is (-0.10092, 0.01744), and this range includes a positive range. Based on domain knowledge, the new estimate is not robust to confounder effects, as we expect price elasticity to be within the negative range.

Based on the heatmap, we can see that a large area of estimates are in the lighter/bright green range, which is close to zero or even positive. Only a small area at the bottom, we would see estimates that are closer to our initial estimate of $-0.06$.

With the findings, the presence of confounders with effects more than ~ -0.48 on the treatment (last second row and above) have high influence on the causal estimate, potentially invalidating the original estimate.

Conclusion

In summary, I have demonstrated both (1) Negative controlled refutation tests and (2) Simulation-based Sensitivity Analysis refutation test. While negative controlled refutation tests are easy to run, we also can employ the use of simulation-based sensitivity analysis to address the validity, robustness and reliabilty of our casual estimates in the presence of unobserved confounders.

Thanks, I hope this simple post was helpful. Have a nice day :)