- Published on
Using Bayesian Workflow in Estimating Price Elasticity
- Authors

- Name
- Kenneth Lim
In the post, I will be using Bayesian Workflow by Gelman et al. (2020) to build a model that estimates the price elasticity causal estimate and predict demand. There's also a very comprehensive guide "Bayesian Modeling and Computation in Python" by Martin et al. (2021) that teaches and explains various foundational concept in Bayesian Modeling.
If you're new to this blog, I've been writing a series of blog posts about modeling price elasticity. You may want to start reading from this first post on data generation: Modeling Via Synthesizing Data. And Vice Versa
When I first started learning bayesian, PyMC is a really convenient library which helped in my learning due to its ease of use, and its expressiveness as a Probabilistic Programming Language (PPL). Fast forward to today, PyMC has really evolved really well. It supports pytensors and can run using other samplers like numpyro. The addition of other support libraries such as arviz also helps organize your bayesian data outputs much more cleanly and provide numerous diagnostic functions to evaluate your work at various stages in the Bayesian Workflow. This makes the bayesian modeling faster, a lot more convenient, and of course more enjoyable.
Prior to staring, we can create a new conda environment and install pymc.
conda create -c conda-forge -n pymc_env "pymc>=5"
1. About Bayesian Workflow
According to Gelman et al. (2020), Bayesian workflow is an iterative, principled approach to model building and inference that integrates domain expertise, data analysis, and model checking. The workflow begins by specifying a preliminary model and prior distributions grounded in substantive knowledge, proceeds through Bayesian fitting to incorporate observed data, and then engages in critical evaluation of results through posterior predictive checks and diagnostics. Findings from these checks inform model refinements, such as adjusting priors or altering model structures, and the process continues until the model reasonably captures patterns in the data without overfitting.
2. Data Preparation
To prepare the data for this modeling, we need to:
- Generate dataset using our
generate_datasetfunction mentioned in previous post. - Normalize/Scale numerical features. MCMC can be very sensitive to magnitude/scale of variables. Not normalizing can lead to numerical instability.
- Remove baseline dummy features. Causes numerical instability as well.
dataset = (
dataset
# Normalize / Scale numerical features
.assign(
demand_norm=lambda d: d.demand / d.demand.mean(),
price_norm=lambda d: d.price / d.price.mean(),
T_t_norm=lambda d: (d.T_t - d.T_t.min()) / (d.T_t.max() - d.T_t.min()),
)
# Remove baseline dummy features
.drop(["D_0", "M_1"], axis=1)
)
d_features = dataset[[c for c in dataset.columns if "D_" in c]].values
m_features = dataset[[c for c in dataset.columns if "M_" in c]].values
3. Modeling with Bayesian Workflow
Gelman et al. (2020) mentions there are two strategies for choosing an initial model: (1) start with a relatively simple model, checking for systematic mismatches through diagnostics and then adding complexity as needed, or (2) start with a more fully specified model that captures as many real-world complexities as possible, and then simplifying the model.
For this, I will start from a simple model and then add more complexity along the way based on observation from the data and feedback from the modeling process.
3.1 Baseline Level Model
First, we can initialize a model with just the level i.e. the average demand, and perform a prior predictive check.
In prior predictive check, we generate data based on just the prior parameters to look at the possible space of data that can be generated. If the generated data covers the actual observations and not too widely, our starting assumptions of the prior are plausible. Whereas, if the generated does not cover the actual data, then we need to fix our prior assumptions.
Let's do that check:
# Base model
with pm.Model() as base_model:
# Level
alpha = pm.Normal("alpha", mu=0.5, sigma=0.1)
# Linear equation
mu = pm.Deterministic("mu", pm.math.exp(alpha))
# Observed data
epsilon = pm.HalfStudentT("epsilon", sigma=0.005, nu=10)
demand_norm = pm.Normal("demand_norm", mu=mu, sigma=epsilon, observed=dataset.demand_norm.values)
with base_model:
idata_prior = pm.sample_prior_predictive(1000)
show_prior_predictive(idata_prior, dataset)

Figure 1a. Prior Predictive Check of Initial Model with Initial Priors. Actual (Red). Blue/Orange (Prediction)
We can see that the prior does not provide any cover for the actuals. Thus, I will need to tune the priors such that it covers actual sufficiently, but not too large of a variance for better mixing performance. After tuning:
# Revised model priors after prior predictive checks
with pm.Model() as base_model:
# Level
alpha = pm.Normal("alpha", mu=0.0, sigma=0.1)
# Linear equation
mu = pm.Deterministic("mu", pm.math.exp(alpha))
# Observed data
epsilon = pm.HalfStudentT("epsilon", sigma=0.005, nu=10)
demand_norm = pm.Normal("demand_norm", mu=mu, sigma=epsilon, observed=dataset.demand_norm.values)
with base_model:
idata_prior = pm.sample_prior_predictive(1000)
show_prior_predictive(idata_prior, dataset)

Figure 1b. Prior Predictive Check of Initial Model with Tuned Priors. Actual (Red). Blue/Orange (Prediction)
This looks considerably more reasonable than the previous check because the observed data (red line) generally falls within the orange band (the prior predictive interval). In other words, the prior assumptions are now better aligned with the actual data. Next, let's run our NUTS sampler, check our diagnostics and do a predictive posterior check.
with base_model:
idata_base = pm.sample(
chains=4,
tune=500,
draws=1000,
return_inferencedata=True,
idata_kwargs={'log_likelihood': True} # Required for az.compare
)
pm.sample_posterior_predictive(idata_base, extend_inferencedata=True)
az.summary(idata_base, var_names=["alpha", "epsilon"])
show_posterior_predictive(idata_base, dataset)
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| alpha | 0.000 | 0.002 | -0.003 | 0.003 | 0.0 | 0.0 | 4274.0 | 3101.0 | 1.0 |
| epsilon | 0.079 | 0.001 | 0.076 | 0.081 | 0.0 | 0.0 | 4354.0 | 2450.0 | 1.0 |

Figure 1c. Posterior Predictive Check of Initial Model. Actual (Red). Blue/Orange (Prediction)
The table provides us with some useful diagnostic statistics:
- (R-hat). Values of 1.01 or lower indicates good mixing/convergence across all chains
- ESS (Bulk and Tail). Effective Sample Size tells us amount of data sampled accounting for autocorrelation. An ESS greater than 400 is recommended as a general rule of thumb.
Since we have for all parameters, this indicate that the samples drawn by MCMC has mixed well and converged across all chains. The effective sample sizes (ESS_bulk and ESS_tail) are large (generally in the thousands or more), signaling that the sampler is efficiently exploring both the main body and the tails of the posterior distribution. Based on this diagnostic, the model appears to be a good fit.
Taking a look at the posterior predictive check chart, the orange band (prediction) appears to capture most of the red (actual) data. However, there are also instances where the observed values deviate outside the interval. Let's see how can we improve the baseline model next.
3.2 Trend Level Model
From here onwards, I will not be showing steps for prior predictive checks, or explaining the diagnostics again to keep this post concise. I will be adding components to the model, and displaying the diagnostics and plots for your reference.
It is apparent that there is a linear trend comparing with the baseline prediction. So let's add our next component to the model.
with pm.Model() as tl_model:
# Level
alpha = pm.Normal("alpha", mu=-0.2, sigma=0.1)
# Trend
phi = pm.HalfNormal("phi", sigma=0.5)
T = pm.Deterministic("T", phi * dataset.T_t_norm.values)
# Linear equation
mu = pm.Deterministic("mu", pm.math.exp(alpha + T))
# Observed data
epsilon = pm.HalfStudentT("epsilon", sigma=0.005, nu=10)
demand_norm = pm.Normal("demand_norm", mu=mu, sigma=epsilon, observed=dataset.demand_norm.values)
with tl_model:
idata_tl = pm.sample(
chains=4,
tune=500,
draws=1000,
return_inferencedata=True,
idata_kwargs={'log_likelihood': True} # Required for az.compare
)
pm.sample_posterior_predictive(idata_tl, extend_inferencedata=True)
az.summary(idata_tl, var_names=["alpha", "phi", "epsilon"])
show_posterior_predictive(idata_tl, dataset)
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| alpha | -0.092 | 0.003 | -0.097 | -0.086 | 0.0 | 0.0 | 1563.0 | 1430.0 | 1.0 |
| phi | 0.181 | 0.005 | 0.171 | 0.190 | 0.0 | 0.0 | 1591.0 | 1541.0 | 1.0 |
| epsilon | 0.059 | 0.001 | 0.057 | 0.061 | 0.0 | 0.0 | 2139.0 | 2235.0 | 1.0 |

Figure 2. Posterior Predictive Check. Actual (Red). Blue/Orange (Prediction)
3.3 Holiday Seasonality Trend Level Model
The next obvious factor is seasonality. I'll be adding both yearly and weekly seasonality, as well as holidays to account for the sharp spikes.
with pm.Model() as hstl_model:
# Intercept
alpha = pm.Normal("alpha", mu=-0.1, sigma=0.1)
# Trend
phi = pm.HalfNormal("phi", sigma=0.2)
T = pm.Deterministic("T", phi * dataset.T_t_norm.values)
# Seasonality
gamma = pm.Normal("gamma", mu=0, sigma=0.1, size=11)
S_m = pm.Deterministic("S_m", pm.math.dot(m_features, gamma))
delta = pm.Normal("delta", mu=0, sigma=0.1, size=6)
S_d = pm.Deterministic("S_d", pm.math.dot(d_features, delta))
# Holiday
theta = pm.HalfNormal("theta", sigma=0.01)
H = pm.Deterministic("H", theta * dataset.H_t.values)
# Linear equation
mu = pm.Deterministic("mu", pm.math.exp(alpha + T + H + S_m + S_d))
# Observed data
epsilon = pm.HalfStudentT("epsilon", sigma=0.005, nu=10)
demand_norm = pm.Normal("demand_norm", mu=mu, sigma=epsilon, observed=dataset.demand_norm.values)
with hstl_model:
idata_hstl = pm.sample(
chains=4,
tune=500,
draws=1000,
return_inferencedata=True,
idata_kwargs={'log_likelihood': True} # Required for az.compare
)
pm.sample_posterior_predictive(idata_hstl, extend_inferencedata=True)
az.summary(idata_hstl, var_names=["alpha", "phi", "gamma", "delta", "theta", "epsilon"])
show_posterior_predictive(idata_hstl, dataset)
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| alpha | -0.106 | 0.006 | -0.117 | -0.095 | 0.0 | 0.0 | 1019.0 | 1467.0 | 1.0 |
| phi | 0.181 | 0.004 | 0.173 | 0.190 | 0.0 | 0.0 | 4960.0 | 2793.0 | 1.0 |
| gamma[0] | -0.009 | 0.006 | -0.021 | 0.003 | 0.0 | 0.0 | 1390.0 | 2344.0 | 1.0 |
| gamma[1] | -0.003 | 0.006 | -0.014 | 0.009 | 0.0 | 0.0 | 1406.0 | 2276.0 | 1.0 |
| gamma[2] | 0.013 | 0.006 | 0.001 | 0.025 | 0.0 | 0.0 | 1284.0 | 2346.0 | 1.0 |
| gamma[3] | 0.030 | 0.006 | 0.019 | 0.042 | 0.0 | 0.0 | 1373.0 | 1766.0 | 1.0 |
| gamma[4] | 0.040 | 0.006 | 0.029 | 0.051 | 0.0 | 0.0 | 1317.0 | 1942.0 | 1.0 |
| gamma[5] | 0.031 | 0.006 | 0.020 | 0.043 | 0.0 | 0.0 | 1379.0 | 1982.0 | 1.0 |
| gamma[6] | 0.011 | 0.006 | -0.000 | 0.022 | 0.0 | 0.0 | 1404.0 | 2145.0 | 1.0 |
| gamma[7] | -0.029 | 0.006 | -0.042 | -0.018 | 0.0 | 0.0 | 1264.0 | 2234.0 | 1.0 |
| gamma[8] | -0.015 | 0.006 | -0.027 | -0.004 | 0.0 | 0.0 | 1381.0 | 2104.0 | 1.0 |
| gamma[9] | 0.002 | 0.006 | -0.009 | 0.014 | 0.0 | 0.0 | 1404.0 | 2221.0 | 1.0 |
| gamma[10] | 0.023 | 0.006 | 0.012 | 0.035 | 0.0 | 0.0 | 1281.0 | 1884.0 | 1.0 |
| delta[0] | -0.015 | 0.005 | -0.024 | -0.006 | 0.0 | 0.0 | 2280.0 | 2897.0 | 1.0 |
| delta[1] | 0.017 | 0.004 | 0.009 | 0.026 | 0.0 | 0.0 | 2311.0 | 3038.0 | 1.0 |
| delta[2] | -0.003 | 0.005 | -0.011 | 0.006 | 0.0 | 0.0 | 2324.0 | 2681.0 | 1.0 |
| delta[3] | 0.021 | 0.005 | 0.013 | 0.030 | 0.0 | 0.0 | 2411.0 | 3057.0 | 1.0 |
| delta[4] | 0.008 | 0.005 | -0.000 | 0.017 | 0.0 | 0.0 | 2200.0 | 2460.0 | 1.0 |
| delta[5] | 0.002 | 0.004 | -0.005 | 0.011 | 0.0 | 0.0 | 2108.0 | 2747.0 | 1.0 |
| theta | 0.051 | 0.006 | 0.042 | 0.062 | 0.0 | 0.0 | 5506.0 | 2844.0 | 1.0 |
| epsilon | 0.053 | 0.001 | 0.052 | 0.055 | 0.0 | 0.0 | 5580.0 | 2918.0 | 1.0 |

Figure 3. Posterior Predictive Check. Actual (Red). Blue/Orange (Prediction)
3.4 Final Model
In our final model, I will add price, and lets find out if we can estimate price elasticity correctly :) (true value = -0.06)
# Add price
with pm.Model() as phstl_model:
# Intercept
alpha = pm.Normal("alpha", mu=-0.1, sigma=0.1)
# Trend
phi = pm.HalfNormal("phi", sigma=0.2)
T = pm.Deterministic("T", phi * dataset.T_t_norm.values)
# Seasonality
gamma = pm.Normal("gamma", mu=0, sigma=0.1, size=11)
S_m = pm.Deterministic("S_m", pm.math.dot(m_features, gamma))
delta = pm.Normal("delta", mu=0, sigma=0.1, size=6)
S_d = pm.Deterministic("S_d", pm.math.dot(d_features, delta))
# Holiday
theta = pm.HalfNormal("theta", sigma=0.01)
H = pm.Deterministic("H", theta * dataset.H_t.values)
# Price
beta = pm.Normal("beta", mu=0.0, sigma=0.01)
P = pm.Deterministic("P", beta * pm.math.log(dataset.price.values))
# Linear equation
mu = pm.Deterministic("mu", pm.math.exp(alpha + T + H + S_m + S_d + P))
# Observed data
epsilon = pm.HalfStudentT("epsilon", sigma=0.005, nu=10)
demand_norm = pm.Normal("demand_norm", mu=mu, sigma=epsilon, observed=dataset.demand_norm.values)
with phstl_model:
idata_phstl = pm.sample(
chains=4,
tune=500,
draws=1000,
return_inferencedata=True,
idata_kwargs={'log_likelihood': True} # Required for az.compare
)
pm.sample_posterior_predictive(
idata_phstl,
extend_inferencedata=True,
)
az.summary(idata_phstl, var_names=["alpha", "gamma", "delta", "phi", "theta", "beta", "epsilon"])
show_posterior_predictive(idata_phstl, dataset)
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| alpha | 0.139 | 0.007 | 0.126 | 0.153 | 0.0 | 0.0 | 1656.0 | 2579.0 | 1.00 |
| gamma[0] | -0.013 | 0.005 | -0.022 | -0.005 | 0.0 | 0.0 | 1381.0 | 2031.0 | 1.01 |
| gamma[1] | -0.004 | 0.004 | -0.012 | 0.005 | 0.0 | 0.0 | 1260.0 | 2353.0 | 1.01 |
| gamma[2] | 0.016 | 0.005 | 0.008 | 0.025 | 0.0 | 0.0 | 1436.0 | 1734.0 | 1.01 |
| gamma[3] | 0.027 | 0.004 | 0.019 | 0.035 | 0.0 | 0.0 | 1209.0 | 2244.0 | 1.01 |
| gamma[4] | 0.034 | 0.004 | 0.025 | 0.042 | 0.0 | 0.0 | 1206.0 | 2013.0 | 1.01 |
| gamma[5] | 0.026 | 0.004 | 0.019 | 0.035 | 0.0 | 0.0 | 1275.0 | 2210.0 | 1.01 |
| gamma[6] | 0.010 | 0.004 | 0.002 | 0.019 | 0.0 | 0.0 | 1174.0 | 2028.0 | 1.01 |
| gamma[7] | -0.031 | 0.005 | -0.040 | -0.023 | 0.0 | 0.0 | 1174.0 | 2323.0 | 1.01 |
| gamma[8] | -0.017 | 0.004 | -0.025 | -0.009 | 0.0 | 0.0 | 1310.0 | 2343.0 | 1.00 |
| gamma[9] | -0.002 | 0.005 | -0.011 | 0.006 | 0.0 | 0.0 | 1321.0 | 2147.0 | 1.01 |
| gamma[10] | 0.017 | 0.004 | 0.009 | 0.025 | 0.0 | 0.0 | 1209.0 | 2190.0 | 1.01 |
| delta[0] | -0.017 | 0.003 | -0.024 | -0.011 | 0.0 | 0.0 | 2148.0 | 2758.0 | 1.00 |
| delta[1] | 0.014 | 0.003 | 0.008 | 0.021 | 0.0 | 0.0 | 2257.0 | 2913.0 | 1.00 |
| delta[2] | 0.001 | 0.003 | -0.005 | 0.008 | 0.0 | 0.0 | 2155.0 | 2518.0 | 1.00 |
| delta[3] | 0.020 | 0.003 | 0.014 | 0.026 | 0.0 | 0.0 | 2045.0 | 2595.0 | 1.00 |
| delta[4] | 0.008 | 0.003 | 0.001 | 0.014 | 0.0 | 0.0 | 2074.0 | 2618.0 | 1.00 |
| delta[5] | 0.004 | 0.003 | -0.003 | 0.010 | 0.0 | 0.0 | 2198.0 | 2698.0 | 1.00 |
| phi | 0.184 | 0.003 | 0.178 | 0.190 | 0.0 | 0.0 | 4429.0 | 3098.0 | 1.00 |
| theta | 0.061 | 0.005 | 0.052 | 0.069 | 0.0 | 0.0 | 4098.0 | 2789.0 | 1.00 |
| beta | -0.058 | 0.001 | -0.061 | -0.055 | 0.0 | 0.0 | 2798.0 | 2968.0 | 1.00 |
| epsilon | 0.039 | 0.001 | 0.038 | 0.041 | 0.0 | 0.0 | 4767.0 | 2875.0 | 1.00 |

Figure 4a. Posterior Predictive Check of Final Model. Actual (Red). Blue/Orange (Prediction)

Figure 4b. Posterior Predictive Check of Final Model [Close Up]. Actual (Red). Blue/Orange (Prediction)

Figure 4c. Posterior Predictive Check of Final Model [De-normalized]. Actual (Red). Blue/Orange (Prediction)
The final bayesian model have managed to estimate the casual effect of price (somewhere close). Note that in this case, even we have scaled the numerical variables, the magnitude of is not changed since the relative ratio of remains the same. We can plot the distribution of the estimated effect and denote the 94% high density interval, along with the true value:
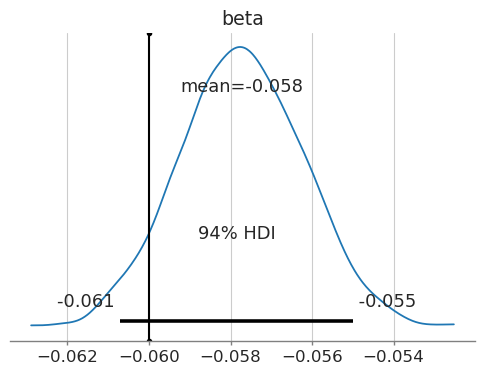
Figure 4d. 94% High Density Interval for price elasticity estimate.
Does this mean we're facing some regularization bias? Indeed. The usage of priors in Bayesian models inherently introduces a form of regularization. There are regularizing priors such as the Laplace Prior, where the parameter values near zero has a much higher probability density, penalizing larger values. Though, we did not explicitly use regularizing priors, the effect of the priors biases is omnipresent.
4. Model Comparison
Lastly, last compare the model performances using az.compare:
az.compare({
"base_model": idata_base,
"tl_model": idata_tl,
"hstl_model": idata_hstl,
"phstl_model": idata_phstl,
})
| rank | elpd_loo | p_loo | elpd_diff | weight | se | dse | warning | scale | |
|---|---|---|---|---|---|---|---|---|---|
| phstl_model | 0 | 3297.298099 | 22.376594 | 0.000000 | 1.000000e+00 | 31.953636 | 0.000000 | False | log |
| hstl_model | 1 | 2753.349218 | 21.106417 | 543.948882 | 1.147469e-07 | 32.092996 | 28.781577 | False | log |
| tl_model | 2 | 2567.295291 | 3.260257 | 730.002809 | 7.801077e-08 | 33.950505 | 32.519977 | False | log |
| base_model | 3 | 2043.436265 | 2.025364 | 1253.861834 | 0.000000e+00 | 30.232995 | 34.777540 | False | log |
The output shows the ranking of models from top (best performing) to bottom (worst performing), using the metric ELPD_LOO, which stands for "Expected Log Predictive Density via Leave-One-Out Cross-Validation".
Expected Log Predictive Density (ELPD). Measure of how good the model’s predictions are on average (in terms of the log of the predictive density). Higher values of ELPD generally indicate better predictive performance.
Leave-One-Out Cross-Validation (LOO). ArviZ leverages Pareto Smoothed Importance Sampling (PSIS-LOO) to efficiently approximate leave-one-out without refitting.
Models with higher elpd_loo suggest better out-of-sample predictive performance. If the difference in ELPD (shown as elpd_diff) is small and the standard error dse around that difference is large, it implies there’s not enough evidence to decisively prefer one model over another.
5. Conclusion
This post was rather long. Though we have merely scratched the surface of Bayesian modeling, I do hope it does give a little insight on how Bayesian modeling can be done using the Bayesian Worflow framework. Here I have briefly shown:
- how to start modeling
- how to use and interpret Prior/Posterior Predictive Checks
- how to check diagnostic statistics to infer whether the MCMC sampling process is acceptable.
- how to observe data and use external knowledge to inform modeling decisions
- how to use the above to determine if the model is a good fit
- Bayesian models do suffer from regularization bias
- how to compare and evaluate model performances with one another
I hope this has been helpful to you. Thanks and till next time!
References: